学习：数据结构——邻接表

在做图论的时候，为了储存图，我们会使用邻接矩阵

就比如上面这个图，用邻接矩阵储存就是这样：

0 1 2 3 4 5

0 0 0 1 0 1 1

1 0 0 0 0 1 1

2 1 0 0 1 1 0

3 0 0 1 0 0 0

4 1 1 1 0 0 0

5 1 1 0 0 0 0

但是这样储存明显有缺点：

空间复杂度太大 $O(n^2)$

时间复杂度太大 $O(n^2)$

于是乎，邻接表你值得拥有
谔谔，查遍oi wiki就找到了两行解释，然后百度百科太权威看不懂
好吧，看看广大人民怎么说：

在网上翻半天翻到的

首先我想说邻接表真是个巧妙的数据结构呵

	0	1	2	3	4	5
0	0	0	1	0	1	1
1	0	0	0	0	1	1
2	1	0	0	1	1	0
3	0	0	1	0	0	0
4	1	1	1	0	0	0
5	1	1	0	0	0	0

邻接表

首先，邻接表跟链表有几分相像，这样就好理解邻接表了

不过我们不用链表，我们只是用数组来模拟邻接表的普通OIer

那么就有以下数组要用：

$u[i]$ 存第 $i$ 条线的起点
$v[i]$ 存第 $i$ 条线的终点
$w[i]$ 存第 $i$ 条线的权值
$first[i]$ 存~~我其实说不清楚~~
$next[i]$ 存~~其实我还是说不清楚~~

还有，设 $n$ 为边数， $m$ 为点数

关于 $u$ , $v$ , $w$ 数组

读入的时候，就把对应的起点、终点、权值存进 $u$ $v$ $w$

关于 $first$ , $next$ 数组

最重要的地方来了，就是 $first$ 和 $next$ 到底是干啥的呢？

关于 $first$

$first$ 数组其实是存起点为第 $i$ 个点的边的编号

拗口？（反正我这么觉得）

实际操作起来就是这样的：

初始化将 $first$ 全部初始化为 $-1$

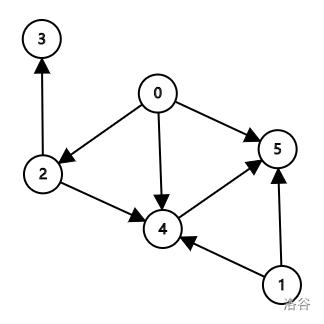
每输入一条边（假设输入的边的编号、起点、终点、权值分别为 $i$ , $u_i$ , $v_i$ , $w_i$ ）， $first[u_i]$ 若等于 $-1$ ，就将 $first[u_i]$ 赋为 $i$

现在根据这个图（权值就看做1）

$u$ $v$ $w$ 可以是这样的（反正什么顺序都一样，就字典序吧）：

$i$	1	2	3	4	5	6	7	8
$u$	0	0	0	1	1	2	2	4
$v$	2	4	5	4	5	3	4	5
$w$	1	1	1	1	1	1	1	1

然后，拿出 $first$ 数组，全部初始化为 $-1$

$j$	0	1	2	3	4	5
$first$	-1	-1	-1	-1	-1	-1

按照步骤，读到 $i=1$ 的时候 $first$ 数组就是这样：

$j$	0	1	2	3	4	5
$first$	1	-1	-1	-1	-1	-1

可以说，邻接表的操作方式真的很迷惑

但接下来就是更迷惑的 $next$ 数组了

关于 $next$

当有两条边的起点一样时（设第一个边编号为 $i$ ，第二个边编号为 $j$ ，公共的起点为 $x$ ，就是说 $u_i=u_j=x$ ）， $next$ 就发挥了作用

如果我们在这种情况下仍然用上面 $first$ 的操作的话，以前的 $first[x]$ 自然会被覆盖掉

所以我们把 $first[x]$ 存到 $next[j]$ 去，再把 $first[x]$ 赋为 $j$

拗口？（反正我还是这么觉得）

实际上就是这样：

初始化时 $next$ 数组全部初始化为 $-1$

每次在输入一条边后，如果 $first[x]$ 不等于 $-1$ ，那就将 $next[j]$ 赋为 $first[x]$ ，再将 $first[x]$ 赋为 $j$

还是接着之前的操作：

$j$	0	1	2	3	4	5
$first$	1	-1	-1	-1	-1	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	-1	-1	-1	-1	-1	-1	-1

按步骤操作到 $i=2$

$j$	0	1	2	3	4	5
$first$	2	-1	-1	-1	-1	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	1	-1	-1	-1	-1	-1	-1

真的非常迷惑

但还没完

我们现在把整个弄完：

手动模拟邻接表

$i=3$

$j$	0	1	2	3	4	5
$first$	3	-1	-1	-1	-1	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	1	2	-1	-1	-1	-1	-1

$i=4$

$j$	0	1	2	3	4	5
$first$	3	4	-1	-1	-1	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	1	2	-1	-1	-1	-1	-1

$i=5$

$j$	0	1	2	3	4	5
$first$	3	5	-1	-1	-1	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	1	2	-1	4	-1	-1	-1

$i=6$

$j$	0	1	2	3	4	5
$first$	3	5	6	-1	-1	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	1	2	-1	4	-1	-1	-1

$i=7$

$j$	0	1	2	3	4	5
$first$	3	5	7	-1	-1	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	1	2	-1	4	-1	6	-1

$i=8$

$j$	0	1	2	3	4	5
$first$	3	5	7	-1	8	-1

$k$	1	2	3	4	5	6	7	8
$next$	-1	1	2	-1	4	-1	6	-1

上面有一个细节，就是 $0 \le j \lt m, 1 \le k \le n$

好了，我们现在存好数组了，那么如何读取呢？

这个费尽心思搞出的储存方式，一定有很好的性能（简洁的算法往往带来低效，复杂的算法往往带来高效）

读取

我们来看，当我们需要遍历以一个点为起点的所有边，我们怎样来读取信息

以 $0$ 为起点为样例：（为了演示就只能用图片了）

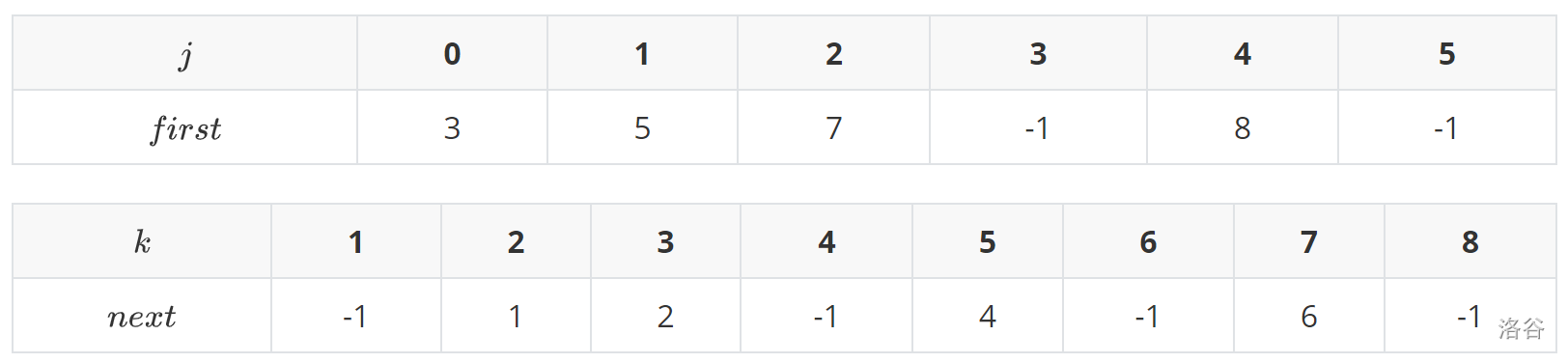
黄的表示起点，蓝的表示边的编号，红的表示下一条边的储存位置，黑的表示读取终止

其中我们从 $first$ 数组的第 $0$ 项读起

下一个边的位置便是当前读到的边的编号

直到读到 $-1$ 为止

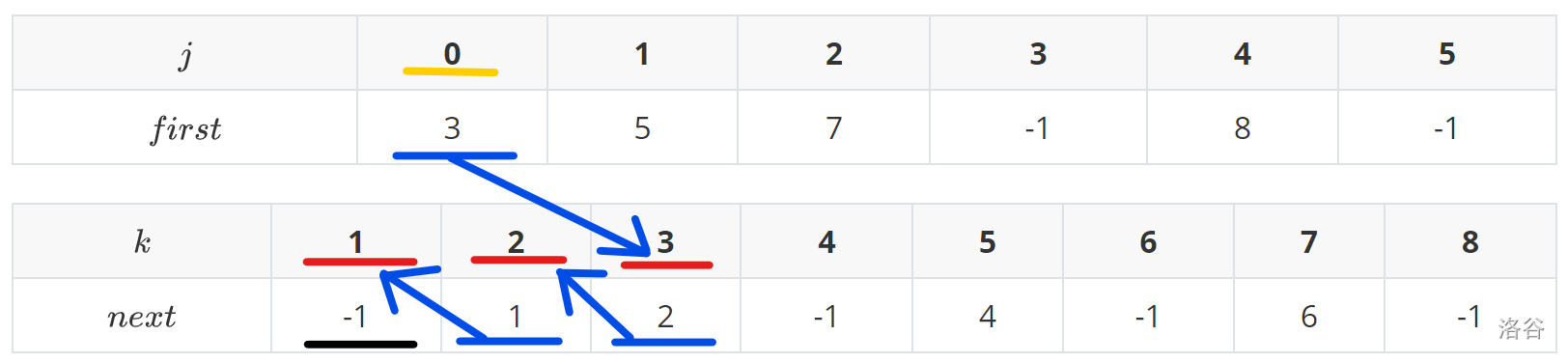
你会发现，读取的效率非常高，因为读取都是一连串读下来，次次读的都是数据

而且空间占用很小

对比一下邻接矩阵，邻接矩阵无地自容

WangYXHaHa

学习：数据结构——邻接表